I wasn’t immediately interested in the symbol of the spiral itself, or in its most obvious meanings. The most interesting approach to this project for me was to deconstruct the definition of a “spiral”, by looking at its properties and possible associations, and highlight those rather than representing it in an obvious way. This interest for came out of considering questions like, “If I use the Fibonacci sequence that is often used to construct spirals, and created a music piece using this sequence, would that mean that I’ve created a new kind of spiral?”. I really want to push the boundaries of what a spiral is.
So I brainstormed what “spiral” meant to me, or what objects/concepts were associated with spirals. I came up with:
- Fibonacci spiral/sequence; Golden Spiral
- Oscillatory movement
- cyclical; repetition (fractal patterns)
- Modelled by equations (mathematical)
- Spiral is the new triangle
- Efficient and stable
- Sacred geometry
- Balance of forces and energy- existence of helical path depends on order and harmony
And so I decided to explore some of these in this body of work.
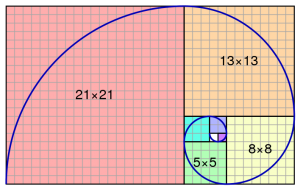
Fibonacci Spiral/Sequence
The Fibonacci sequence is made up of numbers where each figure is the sum of the previous two numbers. In spirals, it is used t construct squares through which the spiral can be drawn. The first few numbers of the sequence are: 1, 1, 2, 3, 5, 8, 13, 21, 34…
The side length of each square is a number from the sequence, and gets progressively bigger. It looks something like this:
Example of how Fibonacci sequence numbers are used to construct a spiral.
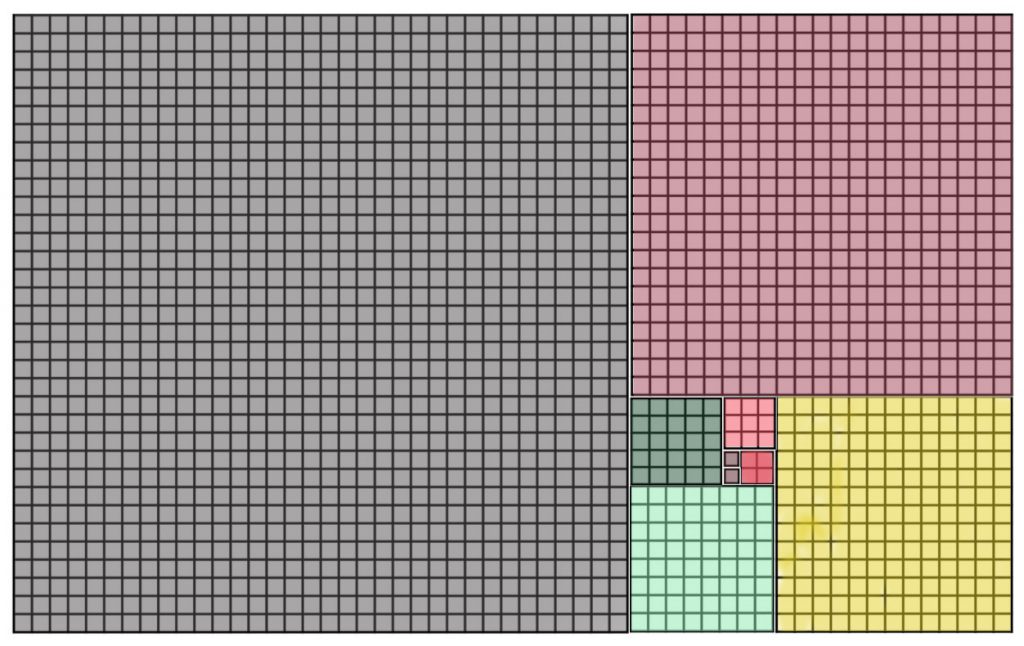
I thought it would be interesting to reconstruct this and remove the spiral and the numbers, to highlight the pattern that is essential to creating this kind of spiral. I also wanted to present this as the spiral itself, blurring the lines between the spiral’s properties and the spiral itself. I used this website: https://incompetech.com/graphpaper/lite/ to construct squares with side lengths from the sequence, up to 34. I then put them all together to create:
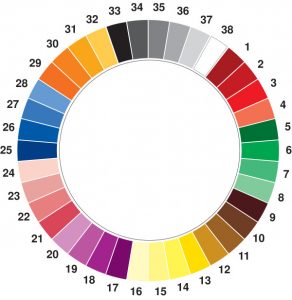
It was difficult to differentiate the different squares, so I decided to colour it. I found a colour wheel with at least 34 different colours, and worked from the Fibonacci sequence to colour the respective squares.
Colour wheel used
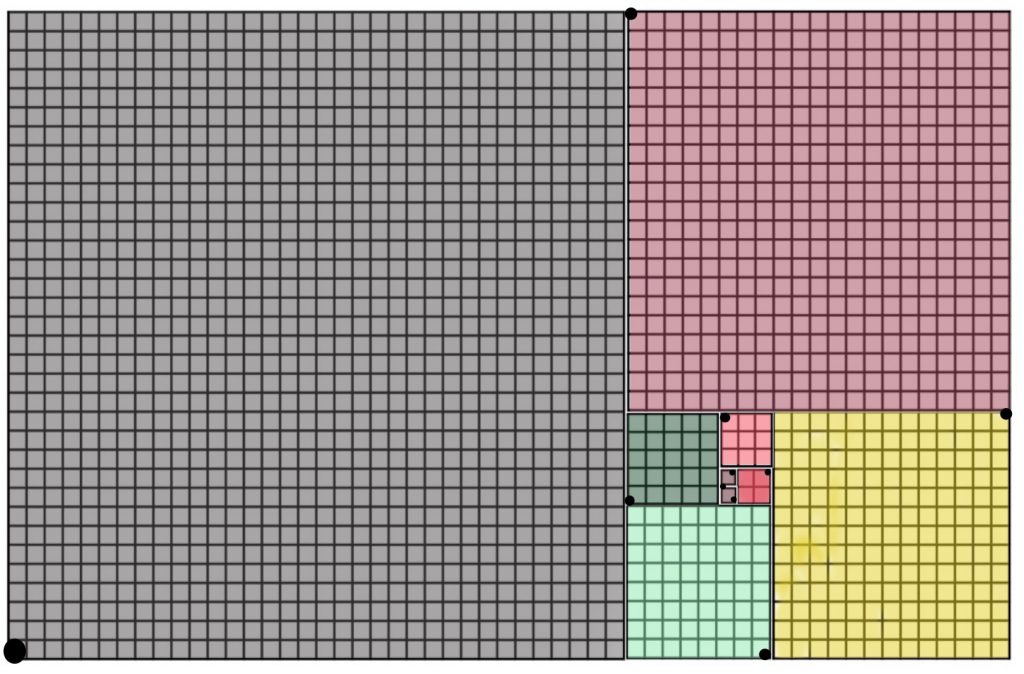
I still felt like the connection between spirals and this image wasn’t as clear as it should’ve been, so I decided to add dots where the spiral line would meet the edges of the squares, to hint at a potential pattern if one were to follow the dots. This gave me the final image to be presented:
Final Fibonacci Sequence Image
I’ve decided to print this on A4 paper to compliment the sizes of the other objects.
Golden Spiral and Golden Ratio
The golden spiral gets wider by a factor of the golden ratio every quarter turn.
Wikipedia definition of Golden Ratio.
The golden ratio is given by a specific irrational number.
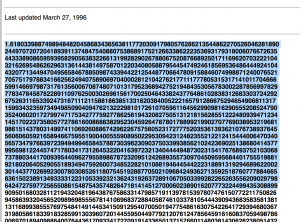
Took the first 21 lines of the golden ratio number. Source: https://www2.cs.arizona.edu/icon/oddsends/phi.htm
I simply decided to use the first 21 lines of the golden ratio number from this particular source as my next piece.
Golden Ratio Number
Golden Angle
Wikipedia definition of Golden Angle
The golden angle is approximately 137.5 degrees, and is used by plants and flowers to efficiently distribute their leaves and florets for maximum exposure using the least amount of effort. I wanted to display this number, is it is important to spirals in nature, in a way that didn’t include simply displaying it. So I thought blocking in the region 0-137.5 degrees on a protractor would do that.
What was presented in class.
Oscillations
I associated oscillatory and repetitive movements with spirals, and so I wanted to represent this oscillatory nature. The simplest way I know to do that is through a pendulum (used heavily in physics). I reused the bob weight I bought, and decided to display it oscillating (swinging) to draw attention to this nature. The dynamic between the string, the weight and gravity also linked in to my interests in the balancing of forces in helical pathways, found in outer space and in atom movements.
What was presented in class.
Cycles
I was struck on how to represent cycles, so I went shopping to see if any seen objects would spark some ideas. I found these metal paper rings, and seeing them stacked next to one another reminded me of cycles and repetition, and they had a nice aesthetic quality to them as well. So I decided to display them as I found them, next to one another. I experimented with how I can display them (whether in a straight line, or a wave shape, etc.), and noticed that the part that was holding them together can be used to imitate the rolling of the circle. I decided to present them in a straight line next to one another, so that a viewer can make the association to movement and repetition.
Final Presentation
Final work presented in class.
I wanted to present them as a collection so that together they can allude to the idea of a “spiral”, without explicitly referring or showing spirals. I think they work much better together than separately.